

|
|
||||||||||||||||||||||||||||||||
How a gyroscope worksCef's Website: click here 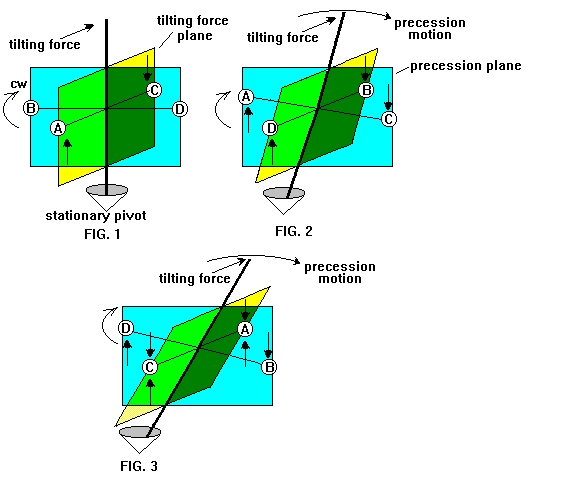 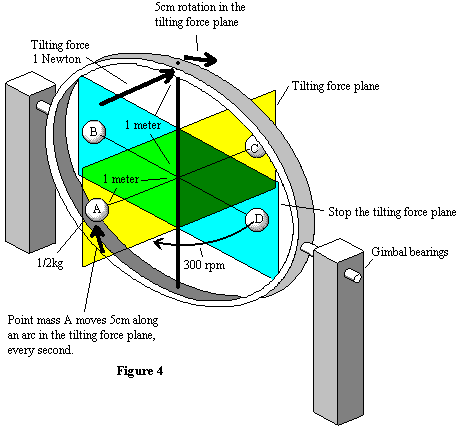 A quick explanation of how a gimbaled gyro functions Figure 4 shows a simplified gyro that is gimbaled in a plane perpendicular to the tilting force. As the rim rotates through the gimbaled plane all the energy transferred to the rim by the tilting force is mechanically stopped. The rim then rotates back into the tilting force plane where it will be accelerated once more. Each time the rim is accelerated the axis moves in an arc in the tilting force plane. There is no change in the RPM of the rim around the axis. The gyro is a device that causes a smooth transition of momentum from one plane to another plane, where the two planes intersect along the axis. A more detailed explanation of how a gimbaled gyro functions Here I attempt to show how much the axis will rotate around a gimbaled axis. That is to say, how fast it rotates in the direction of a tilting force. In figure 4, the precession plane in the gimbaled example functions differently than in the above example of figures 1-3, and I have renamed it "stop the tilting force plane". The point masses at the rim are the only mass of the gyro system that is considered. The mass and gyroscope effect of the axis is ignored. At first consider only ˝ of the rim, the left half. The point masses inside
the "stop the tilting force plane" share half their mass on either side of the
plane, and add their combined, 1/4kg, mass to point mass A of 1/2kg. So then
the total mass on the left side is ˝ the total mass of all 4 point masses, or
1kg. The tilting force will change the position of point mass B and D very
little and change the position of point mass A the most. So we must use the
average distance from the axis of all the mass on the left-hand side.
Point mass A is rotating at 5 revolutions per second. This means that it is exposed to the tilting force for only .1 seconds. The tilting force of 1 Newton, if applied for .1 second, will cause the mass at the average distance to move .005 meter in an arc, in the tilting force plane. Since the length of the axis is twice as long as the average distance of the rim’s mass, the axis will move .01 meter in an arc. At the end of .1 second the point mass will be in the "stop the tilting force plane" and all the energy transferred to point mass A is lost in the physical restraint of the gimbal bearings. The same thing happens when point mass A is on the right side of figure 4. Only now, the tilting force will move point mass A down, and the axis will advance another .01meter. .01 meter every .1 second is not the whole story because the mass on the right side of the gyro hasn’t been considered. The right side has the same mass as the left and has the same effect on the axis as the left side does. So the axis will advance half as much, half of .01 meter, or .005meters. Both halves of the rim mass will pass through the stop the tilting force plane 10 times in one second. Each time a half of the rim passes though the "stop the tilting force plane", it losses all its momentum that was added by the tilting force. The mass has to undergo acceleration again so we continually calculate the effect that 1 Newton has for .1 second on the rim mass at the average distance, 10 times a second. So then; at the point that the 1 Newton force is applied, the axis will move 5cm per second along an arc. The gyro will rotate at .48 RPM within the tilting force plane. What considerations does the rim speed have on the distance that the axis will rotate along an arc in the tilting force plane? The gyro will rotate in the tilting force plane, half as fast if the rim speed is doubled. What happens when the mass of the rim is doubled? The gyro will rotate in the tilting force plane, half as fast if the rim mass is doubled How does the rim diameter effect rotation in the tilting force plane? The gyro will rotate in the tilting force plane, half as fast if the rim diameter is doubled The Math of a gimbaled gyro 1 Newton = 1kilogram 1 meter sec.2 F=ma d=1/2 X (a X t2 ) 1 Newton acting on 1kg will accelerate the mass at a rate of 1 meter sec^2 the time that ˝ the mass of the rim is exposed to the tilting force at 5 revolutions a second is 10 times a second or 1/10; .1 sec The distance, d, the mass will go in .1 sec
The axis is twice as long as the distance from the average distance that the rim mass is calculated from .005 X 2 = .01 meters Now consider the other side of the gyro as acted on by the same 1 Newton
force.
The force will have ten times a second to accelerate the rim mass from a
relative velocity of 0m /sec.
Other experiments with a gyro |