Dictionary Meanings

A heavy rotating wheel, the axis of which is free to turn in any direction, and which can set to rotate in any plane, independently of forces tending to change the position of the axis.

A small heavy wheel or top rotated (usually electrically) at high speed in anti-friction bearings. Any alteration of the inclination of the axis rotation is resisted by a turning movement (gyrostatic moment). It is therefore used as a compass, as a controlling device in aircraft and torpedoes, and, in large sizes, as a ship's stabiliser.

Heavy spinning disk mounted so that its axis is free to adopt any orientation. The fact that a spinning top will stay upright as long as it is spinning fast enough demonstrates the property of gyroscopic inertia: the direction of the spin axis resists change. This means that the gyroscope mounted universally, in double gimbals, will maintain the same orientation in space however its support is turned, a property applied in many navigational devices.

Inertia, the property of matter that causes it to resist any change of its motion in either direction or speed. This property is accurately described by the first law of motion of the English scientist Sir Isaac Newton: An object at rest tends to remain at rest, and an object in motion tends to continue in motion in a straight line unless either is acted upon by an outside force. Passengers in an accelerating automobile feel the force of the seat against their backs overcoming their inertia so as to increase their velocity. As the car decelerates, the passengers tend to continue in motion and lurch forward. If the car turns a corner, a package on the car seat will slide across the seat as the inertia of the package causes it to continue moving in a straight line. Any body spinning on its axis, such as a flywheel, exhibits rotational inertia, a resistance to change of its rotational speed. A force must act upon the wheel to slow or speed up its rotation. The matter in the wheel is constrained to move along a curved path by the molecular forces that hold the wheel together. The speed of the material along the curved path cannot be changed, however, without overcoming its inertia, and this gives rise to rotational inertia. The inertia of spinning objects results in other phenomena, notably the gyroscopic effect. By common experience, inertia is generally related to mass, the amount of matter in a body. A greater force is needed to accelerate a baseball than to accelerate a Ping-Pong ball. The relation is expressed by Newton's second law of motion: Force=mass X acceleration. This equation is the basis of the field of dynamics, the study of moving bodies. According to the formula, the inertia of a body as determined by an acceleration experiment is measured in mass units. Mass, however, is more often measured by its gravitational property, that is, the attractive force it exerts on other masses. If the other mass is the earth, then weight is a measure of mass. T he identity between gravitational mass (measured by attractive force) and inertia (measured by acceleration) is a cornerstone of physics. The fact that inertial force and gravitational force are both directly proportional to mass was first realized and demonstrated by Galileo about 1590. According to Galileo, a light weight and a heavy weight dropped from the top of a tower must strike the ground simultaneously. Modern repetitions of Galileo's experiment performed in the laboratory have failed to reveal any difference between gravitational force and inertial force. Albert Einstein theorized that gravitational forces and inertial forces are identical and that it is impossible to distinguish between them. This equivalence principle is the basis of Einstein's theory of general relativity. According to this theory, local properties of inertia and gravitation are the result of the entire mass of matter in the universe and the space in which it exists. Although the theory of general relativity is not fully accepted, the few experimental tests that scientists have so far been able to conduct have tended to confirm the theory.

Reluctance of a body to change its state of rest or of uniform velocity in a straight line. Inertia is measured by mass when linear velocities and accelerations are considered; and by moment of inertia (q.v.) for angular motions (i.e. rotations about an axis).

A property of matter by which it continues in its existing state of rest or uniform motion in a straight line, unless that state is changed by an external force.

A measure of the resistance offered by a body to angular acceleration. For a given body, the moment of inertia is not unique but depends on the particular axis of rotation chosen. It is defined as Smr2, where m is the mass of the particle in the body and r is its perpendicular distance from the axis.

The square root of the moment of inertia of a body about a given axis, divided by it mass. The radius of gyration is usually denoted by k, so that I=mk2.

A heavy wheel on a revolving shaft used to regulate machinery or accumulate power.

A heavy wheel attached to a shaft (e.g. an engine crankshaft) either to reduce the speed fluctuation resulting from uneven torque, or to store up kinetic energy to be used in driving a punch, shears, etc., during a short interval.

Coriolis force is the inertial force associated with change in the tangential component of a particle's velocity; e.g. suppose a particle moves with a constant speed v, outwards along a particular radius of a horizontal rotating table whose angular velocity is w. The tan- gential velocity of the particle is r.w (where r is the particle's distance from the axis), and is increasing with r. Therefore there is a tangential acceler- ation which turns out to be c, as well a centripetal acceleration of r.w^2. Thus the particle, by d'Alembert's principle, is in equilibrium; the real forces causing the motion are balance by the centrifugal force, m.r.w^2 and the Coriolis force (= mass x Coriolis acceleration = m.w.v) acting in the direction shown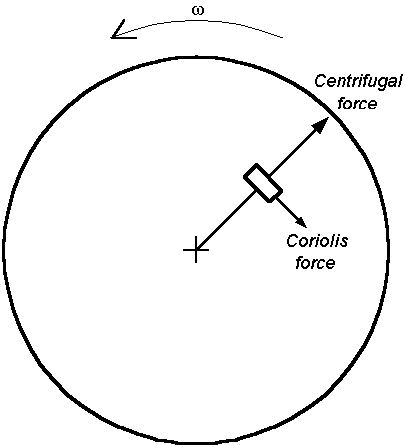